Interception

• Interception is the process by which precipitation is abstracted by vegetation or other forms of surface cover.

• Throughfall is that part of precipitation which reaches the ground after passing through the vegetative cover.

• Interception losses are a function of
  
  
  1. storm character, including intensity, depth and duration;

  2. type, extent and density of vegetative cover,

  3. time of the year (season).

• Annual interception losses, primarily from light storms, can amount to 25% of rainfall.

• For heavy storms, interception losses usually amount to a small fraction of total rainfall.

• For flood studies, the neglect of interception is generally justified on practical grounds.

Infiltration

• Infiltration is the process by which precipitation is abstracted by seeping into the soil below the land surface.

• The infiltrated water moves mostly vertically until it reaches the groundwater table (saturation).

• Groundwater flows laterally (along a piezometric gradient) toward zones of lower elevation, and eventually reaches streams or rivers (baseflow).

• Infiltration is measured in in/hr or mm/hr.

• Rate of infiltration is integrated over the storm duration to obtain the total infiltration (mm or in).

• Average rate is obtained by dividing total infiltration amount by the storm duration.

• Infiltration rates vary as function of the following:
  • The condition of the land surface (crust)

  • The type, extent, and density of vegetative cover

  • The physical properties of the soil, including grain size and gradation

  • The storm character. i.e., intensity, depth, and duration

  • The water temperature

  • The water quality, including chemical constituents and other impurities

  • In general, as a function of physical, chemical, and biological properties of the soil mass.

Infiltration formulas

• Infiltration rates have a tendency to decrease with time.

• This fact led Horton to develop his decay formula for infiltration:

  f= fc + (fo - fc) e-kt

• in which f = instantaneous infiltration rate; f_o = initial infiltration rate; f_c = final infiltration rate; k = a decay constant; t = time.

• This equation has three parameters: initial rate f_o, final rate f_c, and decay constant k.

• With a knowledge of the final rate, two sets of measurements can be solved to give initial rate and constant k.

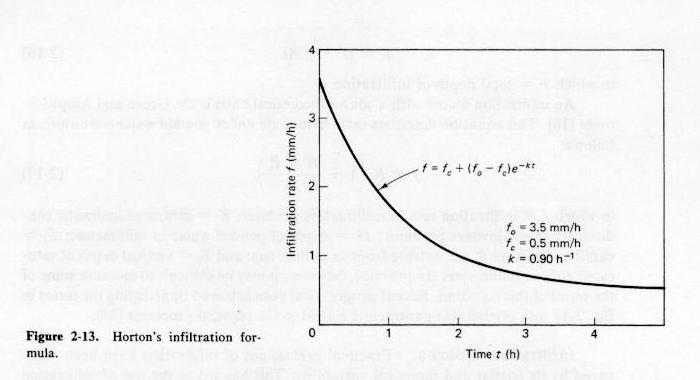
Fig. 2-13

• Typical infiltration rates at the end of 1 hr are shown in Table 2-3.

Table 2-3

Infiltration Index

• Practical evaluations of infltration rate have been hampered by its spatial and temporal variability.

• This has led to the concept of infiltration index.

• Infiltration index assumes that the rate is constant throughout the storm.

• It underestimates the initial rate and may overestimate the final rate.

• Best suited for long-duration storms.

• In this case, the neglect of variation with time is justified in practice.

• φ-index is defined as the constant infiltration rate to be substracted from the prevailing rainfall rate in order to obtain the runoff volume that actually occurred.

• Calculation is by trial and error.

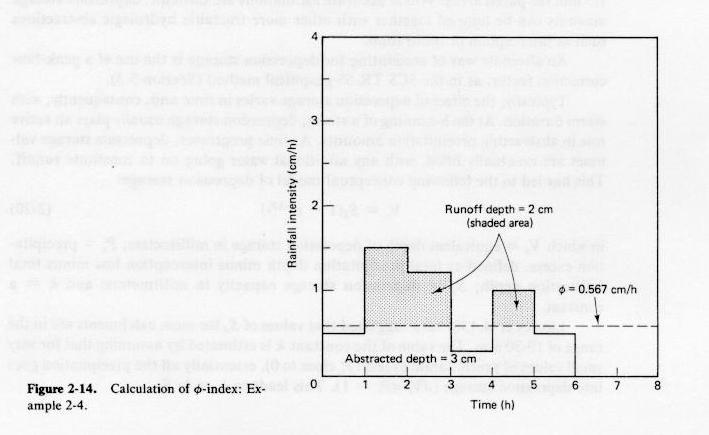
Fig. 2-14

Surface or depression storage

• Surface or depresion storage is the process by which precipitation is abstracted by being retained in puddles, ditches, and other natural or artificial depressions of the land surface.

• Spatial variability of storage in surface depressions precludes its precise calculation.

• Depression storage is inversely related to catchment slope.

• NRCS's TR-55 model uses a surface storage correction factor F to account for depression storage (small ponds occupying less than 5 percent of the catchment area).

• Conceptual model of depression storage:

  Vs = Sd (1- e-kPe)

  in which:

• V_s = equivalent depth of depression storage (mm).

• P_e = precipitation excess; i.e., precipitation minus interception minus infiltration

• S_d = depression storage capacity (mm)

• k = a constant.

• For very small values of P_e, essentially all the precipitation goes into depression storage (dV_s/dP_e = 1).

• Therefore, value of k is estimated as 1/S_d.

Evaporation

• Evaporation is the process by which water accumulated on the land surface is converted into vapor state and returned to the atmosphere.

• Evaporation occurs at the evaporation surface, the contact between water body and overlying air.

• Evaporation refers to the net rate of water loss from the body of water to the atmosphere.

• Evaporation is expressed in mm/day, cm/day, or in/day.

• Evaporation rate is a function of meteorological and environmental factors.

• Those factors important from engineering standpoint are:
  
  
  • Net solar radiation

  • Saturation vapor pressure

  • Vapor pressure of the air

  • Air and water temperatures

  • Wind velocity

  • Atmospheric pressure

• Evaporation rates depend on the climate.

• In the U.S., evaporation rates can vary from 20 inches in Maine to 86 inches in Arizona.

• Methods for determining evaporation:
  
  
  • Water budget

  • Energy budget

  • Mass-transfer techniques

Water budget method

• Assumes that all relevant water-transport phases can be evaluated for a period of time Δt, and expressed in terms of volumes.

• Reservoir or lake evaporation can be evaluated as follows:

  E = P + Q - O - I - ΔS

  in which

  E= volume evaporated from the reservoir

  P = precipitation falling directly into the reservoir

  Q = surface runoff inflow into the reservoir

  O = outflow from the reservoir

  I = net volume infiltrated from the reservoir into the ground

  ΔS = change in stored volume.  

• Precipitation is readily measured.

• Inflow and outflow can be obtained by integrating flow records.

• Net infiltration can be evaluated only indirectly, either by measuring soil permeability or monitoring changes in groundwater level in nearby wells.

• Change in stored volume is determined by means of water stage recorders.

Energy budget method

• During evaporation, significant energy exchanges occur at the evaporating surface.

• A balance of these energy exchanges leads to the energy budget method.

• The amount of heat required to convert one gram of water into vapor, i.e., the heat of vaporization, varies with the temperature.

• At 20^oC, the heat of vaporization is 568 calories.

• Heat must be supplied for evaporation to take place.

   

• Radiation is the emission of energy in the form of electromagnetic waves.

• Solar radiation received at the Earth's surface is a major component of the energy balance.

• Solar radiation reaches the outer surface of the atmosphere at a nearly constant flux of 1.94 cal/cm²/min, of 1.94 langleys/min.

• 1 langley = 1 cal/cm².

• Nearly all of this radiation is of wavelengths in the range 0.3-3.0 μm, with about half in the visible range (0.4-0.7 μm).

• The Earth also emits radiation, but since its surface temperature is about 300^oK, this terrestrial radiation is of much lower intensity and greater wavelength (3-50 μm) than solar radiation.

• It is customary to refer to solar radiation as short-wave radiation, and to terrestrial radiation as long-wave radiation.

   

• The fraction of original solar radiation that reaches the Earth's surface is called direct solar radiation.

• The fraction that is reaches the ground after reflection and scattering is called sky radiation.

• The sum of these two is global radiation.

• Albedo is the reflectivity coefficient of a surface toward shortwave radiation.

• This coefficient varies with color, roughness, and inclination of the surface.

• It is 0.1 for water, 0.1-0.3 for vegetated areas, 0.15-0.4 for bare soil, and 0.7-0.9 for snow-covered areas.

   

• In addition to short wave radiation, there is also a long-wave radiation balance (Figure).

• The Earth also emits radiation, part of which is absorbed and reflected back by the atmosphere.

• The difference between outgoing and incoming fluxes is called long-wave radiation loss.

• At night, long-wave radiation predominates.

• Net radiation is equal to the net short-wave (solar) radiation minus the long-wave (terrestrial) radiation loss.

• Incoming energy:

Qi = Qs (1 - A) - Qb + Qa

in which

Q_i= incoming energy

Q_s = global radiation

A = albedo

Q_b= long-wave radiation loss

Q_a = net energy advected into the waterbody by streams, rain, snow, etc.  

 

• Outgoing energy:

  Qo = Qh + Qe + Qt

  in which

  Q_o = energy expenditure

  Q_h = sensible heat transfer from waterbody to atmosphere by convection and conduction

  Q_e = energy used in the evaporation process

  Q_t = increase in energy stored

• The energy used in the evaporation process is:  

  Qe = ρ Υ E

  in which

  Q_e= energy used in evaporation process (cal/cm²/day)

  ρ = density of water (gr/cm³)

  Υ = heat of vaporization (cal/gr)

  E = evaporation rate (cm/day)

   

  B = Qh / Qe = γ [(Ts - Ta)/(es -ea)] (p/1000)

  in which

  B = Bowen's ratio

  γ = a psychrometric constant equal to 0.66 mb/^oC

  T_s = water surface temperature, ^oC

  T_a = overlying air temperature, ^oC

  e_s= saturation vapor pressure at the water surface temperature, mb

  e_a= vapor pressure at the overlying air temperature, mb

  p = atmospheric pressure, mb  

  E = [Qs (1 - A) - Qb + Qa - Qt] / [ρ Υ (1 + B)]

• The quantities Q_s (1 - A) and Q_b can be measured with radiometers.

• The quantity Q_a can be determined by measuring volumes and temperatures of the water flowing into and out of the body.

• The quantity Q_t is evaluated by periodic measurements of water temperature.

 

Mass-transfer approach

• Evaporation rates are dependent on the temperature of the water surface and the prevailing atmospheric pressure.

• Higher water temperatures result in higher evaporation rates.

• Higher atmospheric pressure results in lower evaporation rates.

• Temperature has a larger effect than atmospheric pressure on evaporation.

• Evaporation rates are a function of the difference between the saturation vapor pressure at the water surface temperature e_s and the vapor pressure of the overlying air e_a (partial vapor pressure).

• The saturation vapor pressure is a function of temperature (Table A-1 and Table A-2).

• The partial vapor pressure can be obtained by multiplying the saturation vapor pressure at the air temperature e_o by the relative humidity of the air (%) and dividing by 100.

   

• As the process of mass-transfer continues, the lowest layer of the atmosphere eventually becomes saturated, and net evaporation reduces to zero and can become negative (condensation).

• Wind carries away water molecules and helps continuous evaporation.

• The Dalton formula considers both vapor pressure gradient and wind effects.

  E = f(u) (es -ea)

• The Meyer formula is an example of mass-transfer evaporation (daily and monthly formulas):

  E = Cd (es -ea) [1 + (W/10)]

  E = Cm (eo -ea) [1 + (W/10)]

 

Penman method (Combination energy budget-mass transfer method)

• Assume p = 1000 mb (close to atmospheric pressure 1013.2 mb).

• Bowen's ratio reduces to:  

  B = γ [(Ts - Ta)/(es -ea)]

• A gradient of vapor pressure and temperature is defined as follows:  

  Δ = (es - eo)/(Ts - Ta)

• Penman in 1945 assumed that the temperatures of water surface and overlying air are equal, and the following statement:  

  Ea / E = (eo - ea)/(es - ea)

  in which:

• E_a = evaporation due only to mass-transfer.

• E = total evaporation.

• Combination of these equations led Penman to:  

  E = (Δ En + γ Ea) / (Δ + γ)

  in which:

  E = total evaporation.

  E_n = evaporation due only to net radiation.

  E_a = evaporation due only to mass-transfer.  

• The radiation part of evaporation is evaluated with Q_n.

• The mass-transfer part of evaporation is evaluated with a mass-transfer equation.  

  E = (α En + Ea) / (α + 1)

• α = Δ/γ is a function of temperature (Table 2-4).

   

• Penman-Monteith 1966 equation is a modification of the Penman equation.  

  Table 2-4

• Monteith explained the physical basis of the mass-transfer formulas such as Dalton's.

• This enabled a better calculation of the mass-transfer evaporation rate and improved the combination model of Penman's.

 

Evaporation determinations using pans

• Evaporation pan is a device to measure evaporation by monitoring the loss of water in a pan during one day.

• It provides an integrated effect of net radiation, wind, temperature, and humidity on evaporation from an open surface.

• The measurement is likely to be somewhat greater than the actual evaporation.

• The ratio of lake-to-pan evaporation is an empirical constant referred to as pan coefficient.

 

Evapotranspiration

• Evapotranspiration is the process by which water in the land surface, soil, and vegetation is converted into vapor state and returned to the atmosphere.

• Evaporation refers to bodies of water; evapotranspiration refers to evaporation from an ecosystem, comprising water, soil, and vegetation.

• Transpiration is the process by which plants transfer water from the root zone to the leaf, providing turgor (the capability of remaining erect).

• Osmotic pressures at root level move water into the roots.

• Water is transported through stem to proximity of leaf surface.

• Air enters leaf surface through small openings called stomata.

• Chloroplasts within the leaves use carbon dioxide from the air and small amounts of the available water to manufacture biomass.

• Water escapes through the stomata as air enters.

• Ratio of water evapotranspired to that used in biomass production is very large (about 800 or more).

• Transpiration occurs continuously, but it is limited by the rate at which moisture becomes available to plants.

• Some authorities believe that transpiration is independent of soil moisture as long as the latter is above the permanent wilting point.

• Others believe that transpiration is proportional to soil moisture.

• Transpiration amounts are a function of the same meteorological and climatic factors that control evaporation rates.

• Evapotranspiration includes all the water returned to the atmosphere from an ecosystem.

   

• Potential evapotranspiration (PET) is the amount that would take place under the assumption of an ample supply of moisture at all times.

• PET is an indication of optimum crop water requirements.

• Reference crop evapotranspiration (ET_o) is the rate from an extended surface of 8-15 mm tall green grass cover of uniform height, actively growing, completely shading the ground, and not short of water.

• Potential evapotranspiration is equivalent to the evaporation of a body of water with negligible heat storage capacity.

• Methods to calculate one overlap the other.

• Penman method is used for both evaporation and evapotranspiration.

• Evapotranspiration models are of several types:
  
  
  • Temperature models

  • Radiation models

  • Combination models

  • Pan-evaporation models.

 

Temperature models to estimate evapotranspiration

• The Blaney-Criddle formula has been used to estimate crop water requirements.

  f = p (0.46 t + 8.13)

• in which

  • f = daily consumptive use factor (mm)

  • p = ratio of mean daily daytime hours for a given month to total daytime hours in the year (%), a function of latitude (Table A-3) [average monthly value = (100%)/12 = 8.33%; daily value at 0^o latitude, 8.33/30.4 days/mo= 0.27]

  • t = mean daily temperature (^oC)

• Consumptive water requirement is the consumptive use factor f times a crop coefficient k_c. (Table 2-5)

   

• Doorenbos and Pruitt have proposed a modification of the Blaney-Criddle formula:

  ETo = a + bf

  in which

• ET_o = reference crop evapotranspiration

• a and b = constants that vary with actual insolation time (ratio n/N between actual and maximum possible bright sunshine hours), minimum relative humidity (%), and daytime wind speed (m/s).

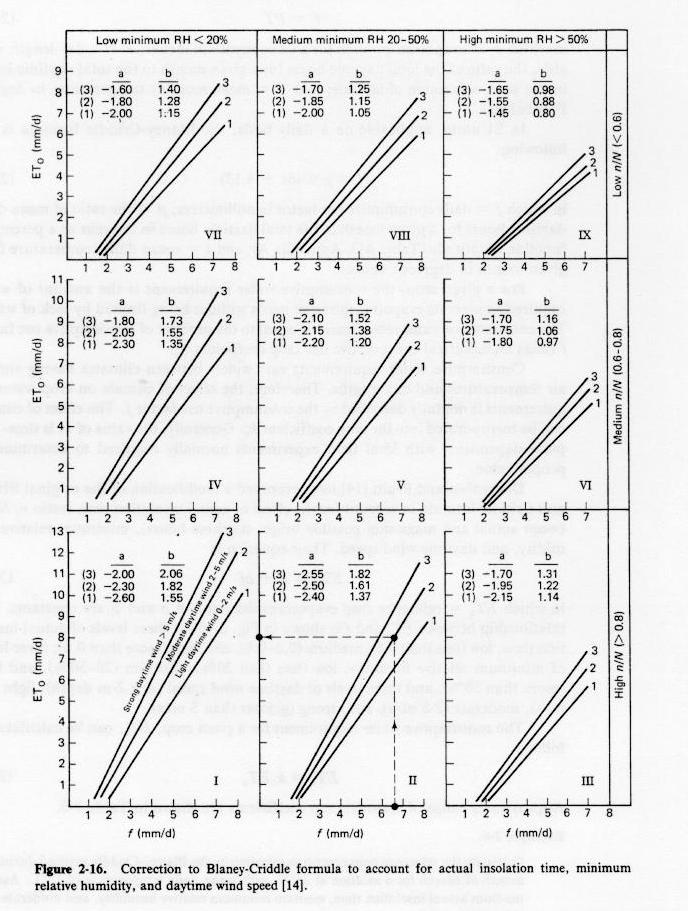
Fig. 2-16

 

• The consumptive water requirement for a given crop is:

  ETc = kc (ETo)

• k_c varies with each crop, from 0.15 to 1.1 (Table 2-5).  

• The Thornthwaite method is also widely used to estimate potential evapotranspiration.

• The method is popular because it is based only on temperature, which is widely available.

• The method is based on an annual temperature efficiency index J, defined as the sum of 12 monthly values of heat index I.

• Each monthly index I is a function of mean monthy temperature T, in ^oC:

  I = (T/5)1.514

• Evapotranspiration at zero latitude PET(0) in cm/month is calculated by the following formula:

  PET(0) = 1.6 (10T/J)c

  c = 0.000000675 J3 - 0.0000771 J2 + 0.01792 J + 0.49239

• At other latitudes, evapotranspiration PET (in cm/month) is calculated by the following formula:

  PET = K [PET(0)]

• K is a constant for each month of the year, varying as a function of latitude (Table A-4).

 

Radiation models

• Priestley and Taylor proposed that potential evapotranspiration be taken as the radiation part of the Penman equation, affected with an empirical constant.

  PET = 1.26 Δ [Qn/(ρ Υ)] / ( Δ + γ)

  PET = 1.26 α [Qn/(ρ Υ)] / ( α + 1)

• However, the constant 1.26 may vary with climatic conditions (it has been reported to be 1.7 in arid regions).

 

Combination models to estimate evapotranspiration

• The original Penman model provided an estimate of evaporation from a free surface.

• Experimental crop coefficients were suggested to convert to evapotranspiration.

• These coefficients (0.6 in the winter and 0.8 in the summer) were intended to multiply the evaporation to get evapotranspiration.

• Other studies have suggested that free-water-surface evaporation and evapotranspiration are nearly the same.

• It seems that energy-budget and mass-transfer components compensate themselves to make evaporation and evapotranspiration nearly equal.

• Potential evapotranspiration correlates well with combination data such as solar radiation and wind velocity.

• Pan evaporation models are also used in evapotranspiration studies.

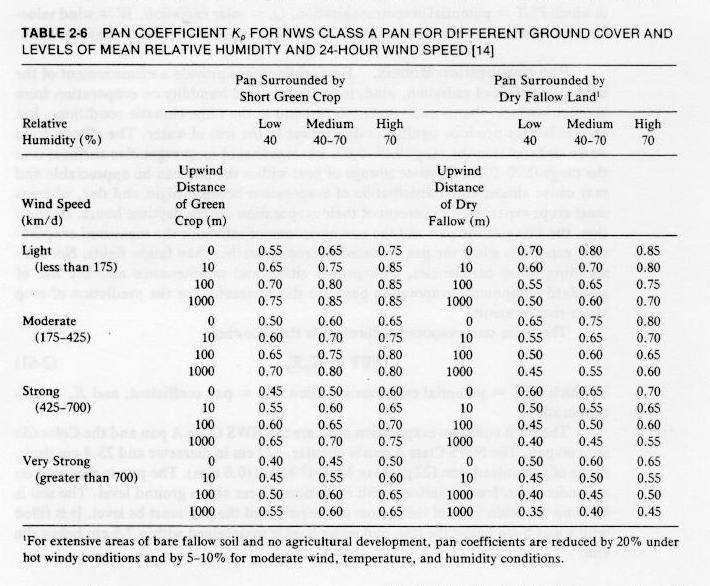
Table 2-6

• NWS Class A pan is generally used for estimating potential evapotranspiration.

Fig. 3-3

 

Go to Chapter 2C.

050202